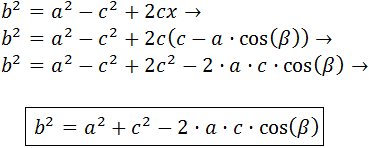Teorema del Coseno

Teorema del coseno

Sea un triángulo cualquiera con lados a, b y c y con ángulos interiores

α

β

γ

(son los ángulos opuestos a los lados, respectivamente).

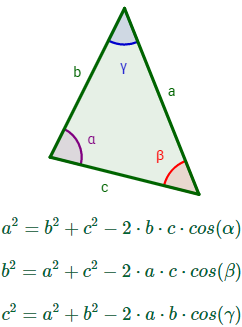
Entonces, se cumplen las relaciones

El teorema del coseno (con demostración). Problemas resueltos de aplicación del teorema del coseno: calcular lados, ángulos y áreas de triángulos. Problemas resueltos y explicados paso a paso. Trigonometría. Bachiller.

Haremos la demostración por el teorema de Pitágoras, pero demostraremos únicamente la fórmula

$�^{2} = �^{2} + �^{2} - 2 � � \cdot � � � (�)$

para el caso en el que el lado b es adyacente a dos ángulos agudos (como en la imagen siguiente). En los otros casos, se procede de forma similar.

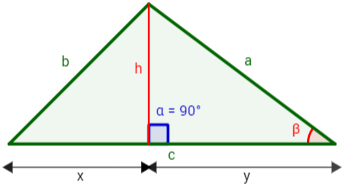
Hemos dividido el triángulo en dos triángulos rectángulos. Observemos que el lado c es

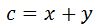
de donde

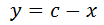
Aplicando el teorema de Pitágoras al triángulo de la izquierda, obtenemos la relación

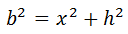
y aplicando Pitágoras al triángulo de la derecha,

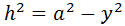
Escribimos en esta última relación y como c - x:

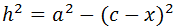
Sumamos las dos relaciones obtenidas:

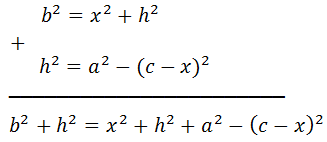
Simplificamos la expresión:

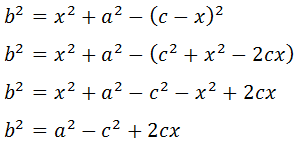
Finalmente, puesto que el triángulo de la derecha es rectángulo, por definición del coseno,

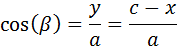
Despejamos x:

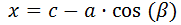
Sustituimos esta x en la expresión que teníamos:

Entradas populares de este blog

Razones Trigonometricas

Las razones trigonométricas son relaciones entre los lados de un triángulo rectángulo que determinan sus ángulos. Este concepto está relacionado con operaciones matemáticas como el seno, coseno y tangente. Las seis razones trigonométricas en un triángulo rectángulo son: seno, coseno, tangente, secante, cosecante y cotangente. Veamos una por una cómo se calculan estas razones y qué relación hay entre ellas. Seno: El seno de un ángulo es la relación entre el cateto opuesto y la hipotenusa. Para ayudarnos a recordar esto, podemos memorizar las siglas SOH, que indican que el Seno es el Opuesto sobre Hipotenusa. El seno se abrevia comúnmente como sin, o a veces como sen. Es también la inversa de la cosecante, o la división entre coseno y cotangente: Coseno: El coseno de un ángulo es la relación entre el cateto adyacente y la hipotenusa. Es decir, el Coseno es el Adyacente sobre Hipotenusa, o CAH: El coseno se abrevia como cos, y es también la inversa de la secante, o la división entre seno ...

Clasificación de triángulos según sus lados

Clasificación de los triángulos según sus lados Triángulo equilátero: Los triángulos equiláteros son aquellos que tienen sus tres lados iguales, y debido a que tienen sus tres lados iguales también tienen sus tres ángulos iguales. Construcción: Triángulo isósceles: Los triángulos isósceles son aquellos que tienen sólo dos de sus lados iguales. Construcción: Triángulo escalen o: Los triángulos escalenos son aquellos que tienen sus tres lados desiguales. . Construcción:

Clasificación de triángulos según su ángulo

Los ángulos de los triángulos Los triángulos, como se puede intuir por su nombre, tienen siempre tres ángulos. Estos ángulos siempre suman 180º, sin importar de qué tipo de triángulo estemos hablando. Los obtusángulos Los rectángulos Los acutángulos Triángulo rectángulo: Son triángulos que tienen un ángulo recto (de 90 grados). En este caso, y para profundizar en la teoría, el lado opuesto a este ángulo de 90 tiene el nombre de hipotenusa y los otros dos lados se le llama catetos. Hay que tener en cuenta, que la hipotenusa siempre será mayor que los catetos de este triángulo. Asimismo, en un triángulo rectángulo los dos ángulos agudos (menores de 90 grados) son complementarios y su suma siempre debe dar en 90 grados. Triángulos acutángulos: Son triángulos que están formados por tres ángulos agudos; es decir, todos sus ángulos miden menos de 90 grados. Triángulos obtusángulos: Como su nombre lo indica, son triángulos que tienen un ángulo obtuso; es decir, mayor de 90 grados....

MateAyudas

Buscar este blog